算法分析

$a[][]$数组是$b[][]$数组的前缀和数组，那么$b[][]$是$a[][]$的差分数组

原数组： $a[i][j]$

我们去构造差分数组： $b[i][j]$

使得$a$数组中$a[i][j]$是$b$数组左上角$(1,1)$到右下角$(i,j)$所包围矩形元素的和。

如何构造$b$数组呢？

我们去逆向思考。

同一维差分，我们构造二维差分数组目的是为了 让原二维数组$a$中所选中子矩阵中的每一个元素加上$c$的操作，可以由$O(n*n)$的时间复杂度优化成$O(1)$

已知原数组$a$中被选中的子矩阵为 以$(x_1,y_1)$为左上角，以$(x_2,y_2)$为右下角所围成的矩形区域;

始终要记得，$a$数组是$b$数组的前缀和数组，比如对$b$数组的$b[i][j]$的修改，会影响到$a$数组中从$a[i][j]$及往后的每一个数。

假定我们已经构造好了$b$数组，类比一维差分，我们执行以下操作 来使被选中的子矩阵中的每个元素的值加上c

$b[x1][y1] += c;$

$b[x1,][y2+1] -= c;$

$b[x2+1][y1] -= c;$

$b[x2+1][y2+1] += c;$

每次对$b$数组执行以上操作，等价于：

for(int i=x1;i<=x2;i++)
  for(int j=y1;j<=y2;j++)
    a[i][j]+=c;

我们画个图去理解一下这个过程：

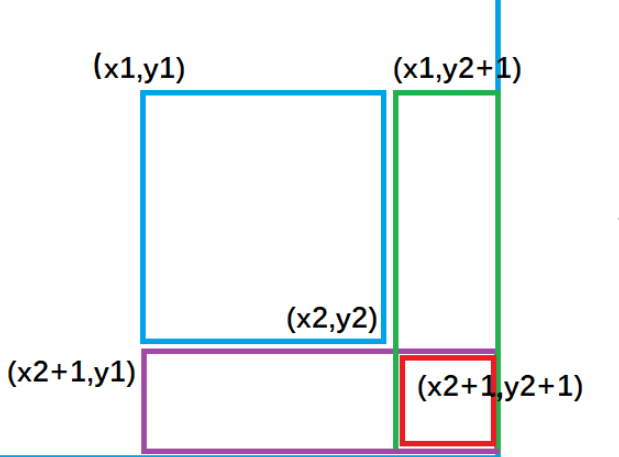
$b[x1][ y1 ] +=c$ ; 让整个$a$数组中蓝色矩形面积的元素都加上了$c$。

$b[x1,][y2+1]-=c$ ; 让整个$a$数组中绿色矩形面积的元素再减去$c$，使其内元素不发生改变。

$b[x2+1][y1]- =c$ ; 让整个$a$数组中紫色矩形面积的元素再减去$c$，使其内元素不发生改变。

$b[x2+1][y2+1]+=c$;让整个$a$数组中红色矩形面积的元素再加上$c$，红色内的相当于被减了两次，再加上一次$c$，才能使其恢复。

代码实现

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int a[N][N],b[N][N];
void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1]+=c;
    b[x1][y2+1]-=c;
    b[x2+1][y1]-=c;
    b[x2+1][y2+1]+=c;
}
int main()
{
    int n,m,q;
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++) //通过原数组构造差分数组
    {
        for(int j=1;j<=m;j++)
        {
            int x;
            cin>>x;
            insert(i,j,i,j,x);
        }
    }
    while(q--) //进行差分操作
    {
        int x1,y1,x2,y2,c;
        cin>>x1>>y1>>x2>>y2>>c;
        insert(x1,y1,x2,y2,c);
    }
    for(int i=1;i<=n;i++) //得到差分数组的前缀和
    {
        for(int j=1;j<=m;j++)
        {
            a[i][j]=a[i][j-1]+a[i-1][j]-a[i-1][j-1]+b[i][j];
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            cout<<a[i][j]<<" ";
        }
        cout<<endl;
    }
    return 0;
}